It turns out that it’s easier to test out some code than it is to write about that code in detail. As a result, this blog is lagging a bit behind the progress of the perfect bracket programming challenge. It’s probably a good time for an update, though, so here’s a bit of information on my first attempts at generating a perfect bracket.

As I mentioned in my first post, the odds of picking a perfect bracket are somewhere between roughly 1 in a billion and 1 in 100 billion. One possible conclusion to draw from this is that it will take somewhere between 1 billion and 100 billion brackets in order to find the perfect one.

This intuition turns out not to be correct. These estimates, from FiveThirtyEight forecasts and from DePaul professor Jeff Bergen, are the probability of the most likely bracket being perfect. Specifically, those estimates are trying to measure the probability that the favorite will win every game. As we know from watching March Madness in previous years, there have always been plenty of upsets, and thus the all-favorites bracket has never come anywhere close to being perfect.

Here’s another incorrect conclusion to draw from this: because the NCAA tournament is much more likely to have, say, 12 upsets than 0, then it must be “better” to predict a bracket with 12 upsets than one with 0 if you’re trying to be perfect. It may initially seem impossible for the all-favorites bracket to be the most likely bracket, while also being much less likely than having 12 upsets in the tournament.

However, here is another way of looking at the problem that shows why these two ideas are still compatible. If we assume that every game has one team whose winning would be considered an “upset” (maybe not realistic in, say 8 vs. 9 seed games, but still a reasonable idea), then the number of ways for there to be 12 upsets is equal to the number of ways to choose 12 games out of a collection of 63. This number, known as 63 choose 12 and equal to about 2.7 trillion, is the number of ways for 12 upsets to occur in the tournament. It is far more likely for the tournament to have 0 upsets than for any one of these outcomes to occur, but it is not 2.7 trillion times more likely, so the “12 upsets” outcome, whose probability is equal to all of those 2.7 trillion probabilities put together, ends up being more likely than the single outcome with no upsets at all.

This has some implications for both individual people filling out brackets and my bracket challenge. Just because there’s usually, say, at least one 13-seed in the second round, doesn’t mean that you should pick one. You’ll look really cool if you get the prediction right, but this only happens because there are a lot of opportunities for it to happen. There are 4 ways for a 13 seed to win but only 1 way for all of them to lose, so you’re still usually better off picking 4 4-seeds than picking a 13.

For my challenge, it means that I need to be careful to pick the most likely brackets rather than ones that just look reasonable. Picking out all of the most likely brackets as quickly as possible will be key to the success of the challenge.

Probabilities for the Project

With that tangent about likely brackets out of the way, I’ll describe my first attempt at finding a perfect bracket. The challenge can be divided into two main parts: writing out as many brackets as possible as fast as possible, and being careful to choose the brackets that are the most likely to happen.

So far, I’ve been running my program on this year’s NCAA tournament. I told the program who is playing in the tournament and what the initial bracket looks like, but not the outcomes of the games, so I can simulate what it will be like next year, when the program will be trying to produce brackets between the tournament selection show and the start of the first round of games.

In order to ensure that I’m choosing the most likely brackets, I will need some way to compute probabilities of various outcomes. I may end up trying to produce my own model, but for now, I’m taking data from FiveThirtyEight. Every year, at the beginning of the tournament, they release their March Madness projections. In these projections, each team is given a rating, and the probability of either team winning a game is based on the difference between the teams’ ratings. In particular, they use this relatively simple formula for the probability of team 1 beating team 2:

where is team 2’s rating and is team 1’s rating. This is a slight modification of the probabilities that form the foundation for the Elo rating system used most notably in chess ratings.

There are a few problems with this system, most notably in how it handles upsets. At the start of the 2022 tournament, 2-seed Duke had a rating of 89.3, and 8-seed North Carolina had a rating of 84.0, giving Duke a 72% chance to win that matchup. By the time they played each other in the final four, their ratings were 92.7 and 90.0, giving Duke just a 62% chance. UNC won the game and advanced to the final.

Of course, I cherry-picked a game in which the underdog won, but this is a pattern that comes up often when a team has multiple upset wins during the tournament. When a team like 2022 Duke wins a few tournament games, their rating doesn’t change much, since they were expected to win (Duke was the better seed in every game they played in that tournament). When a team like 2022 UNC makes a run (they upset a 1 seed and a 4 seed in the early rounds), their rating goes up quite a bit more. The ratings of the remaining teams tend to converge toward each other as the tournament goes on for this reason, so using ratings from the beginning of the tournament to try to predict later rounds will tend to underestimate the chance of upsets later on.

The First Attempt

With those probabilities (and caveats on accuracy) in mind, I wrote a program to try to produce as many likely brackets as possible. What I would like to do is just write out the brackets in order of likelihood: write out the most likely bracket, then the second most likely, and so on. I just get the program to do this for three and a half days, and once the time runs out and the first round of games is about to start, I turn the program off after it’s written the n most likely brackets, for some (hopefully) large value of n.

The main problem with this is that it is very difficult to figure out the most likely brackets in order. Pretty much the only way to do it successfully is to write out all of the brackets, calculate their probabilities of occurring, and then sort that list in order of probability. If it were possible to just write out all of the brackets in three and a half days (let alone sort them), then this project would be too easy. Furthermore, the point of this project is to write brackets. If I’m writing out brackets, computing their probabilities, and then sorting them, I would be much better off just skipping those last two steps and writing more brackets.

Thus, my approach will try to combine the approach of carefully choosing the most likely brackets with the speed of just blindly writing brackets without checking. I will do this by dividing the bracket into 3 sections:

1. Left half of the bracket, first two rounds (24 games)
2. Right half of the bracket, first two rounds (24 games)
3. The last four rounds of the tournament (15 games)

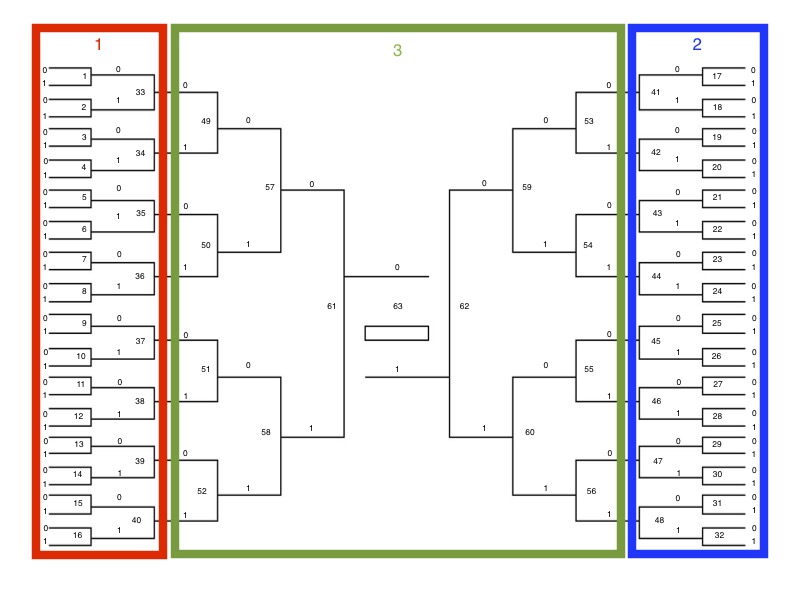
While there are too many overall brackets to ever have any chance of writing them all out, each section is small enough to consider every possible outcome individually. Sections 1 and 2 each consist of 24 games, so there are 2^24=16,777,216 possible ways for each of those sections to go. Once the results of the first two rounds are determined, there are 2^15=32,768 possible outcomes for section 3. These are large numbers, but are very manageable for a computer. Dividing up the bracket this way gives the following approach to generating brackets:

1. Write out all 16,777,216 possible outcomes for section 1 of the bracket, and compute the probabilities of each of these outcomes occurring using FiveThirtyEight’s model.
2. Sort the possible outcomes of section 1 from most to least likely.
3. Repeat steps 1 and 2 for section 2 of the bracket.
4. Combine the most likely outcome of section 1 with the most likely outcome of section 2. Then combine these first 2 rounds of the tournament with the 32,768 possible outcomes for section 3, and use these to create 32,768 completed brackets. Then write these 32,768 brackets to a file. We have created our first completed brackets.
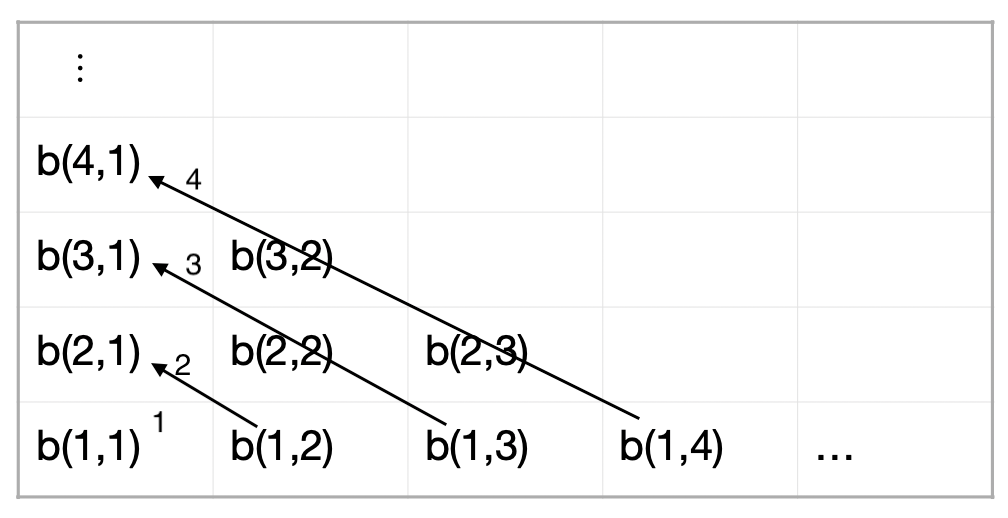
5. Repeat step 4, but with different combinations of results from sections 1 and 2. If b(i,j) is the partial bracket formed by combining the ith most likely outcome of section 1 with the jth most likely outcome of section 2, then step 4 gave us all 32,768 possible brackets with b(1,1) as the outcome of the first two rounds. We are going to repeat step 4 with b(1,2), b(2,1), b(1,3), b(2,2), b(3,1), b(1,4), etc. For every sum k>1, and every i and j such that i + j = k, we will produce all 32,768 brackets with first two rounds b(i,j). We start at k = 2 and keep increasing k until the program runs out of time.

After running this program for about a day and a half, I generated many billions of brackets but a perfect bracket probability of only a few tenths of a percent. While this is far from what I would need to have a decent shot at a perfect bracket, I found this to be a promising result for a few reasons. First, I was putting the program under worse conditions than it would be under during the actual bracket challenge next year. The main point of blindly including all 32,768 possible outcomes of the last 4 rounds of the tournament is for speed: it’s much faster to just write down 32,768 brackets than to actually calculate their probabilities. However, since I was testing the model, I actually went ahead and computed those probabilities to see how the program was doing. During the real thing, I won’t have to do this, which will speed the program up.

Second, the current form of the program leaves a lot to be improved. Blindly printing 32,768 brackets at a time is good for speed, but it results in a lot of extra brackets being written down that have very little chance of happening (even less of a chance than one would normally have of picking a perfect bracket). Historically, a tournament is less likely to have a champion seeded 4 or lower than it is to have a 13 seed in the sweet 16, but at least a quarter of my brackets will have such a team as its champion.

There’s also a more subtle issue in the way that I’m choosing which outcomes to consider. Which of the following is more likely?

• Section 1 has its most likely outcome, and section 2 has its 999th most likely outcome
• Section 1 and section 2 each have their 500th most likely outcomes

It’s far from obvious, but it turns out that the first event is far more likely than the second, and this difference becomes more exaggerated as we move further down the list of the most likely outcomes. However, my program is currently treating these as equally likely, and adding them to the list of brackets at around the same time. I could do a much better job by, say, including b(1,2000) before b(500,500). This is probably important enough for me to write a post on this phenomenon later on.

The third, and possibly most important effect (if the least interesting) is that my choice of programming language could have a major effect on the speed of the program. I’ve been using python so far, but while python is easier to use, it tends to run much more slowly than something like C++ or even Java, so I could probably speed things up quite a bit by switching. I’ll probably work on this once I start running out of improvements to make on the bracket generation process.

I’ve already made some improvements on my approach, but the same basic idea remains: divide up the bracket into sections, get every possible outcome for the early rounds, and then extend the most likely outcomes into the later rounds. The project is hopefully on its way to constructing a perfect bracket!